数理教研室瞿娟老师开设《复数相等与共轭复数》公开课
2024年9月9日上午第四节课,瞿娟老师在2361班开设题为《复数相等与共轭复数》的公开课.学校吴晓进、吴萍、葛玲芳等人参与听评课活动.
本课按内容选定——任务导学——合作探究——交流研讨——归纳提升——反馈巩固六个环节的思路展开授课.先从数集的扩充开始,再通过2个简单的问题引入课题,学生思考,引发学生得出答案,探索复数相等的充要条件以及共轭复数的概念,让学生主动参与教学中,学习兴趣较高.
评课环节,大家一致认为能够生随师动,条理清晰,效果很好.


教 案
课 题 |
9.1.2复数相等与共轭复数 |
授课时间 |
|
学习目标 |
1.理解复数相等的充要条件; 2.理解共轭复数的概念,会求共轭复数 3.了解复数在电工学上的应用. |
教学重点 |
复数相等的充要条件,共轭复数的概念 |
教学难点 |
复数相等的充要条件,共轭复数的概念 |
教学准备 |
PPT |
教 学 过 程 |
教学内容 
一、问题探究
二、抽象概括
复数相等的充要条件
三、例题讲析
四、合作交流
五、抽象概括
共轭复数的概念
|
教 师 活 动
一、问题探究 两个实数可以比较大小,任意两个复数也可以比较大小吗?两个复数相等的条件是什么? 事实上,不是任意两个复数都可以比较大小的. 二、抽象概括(一) 一般地, (1)实数与虚数之间、两个虚数之间不能比较大小. (2)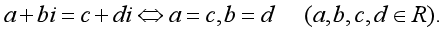 即:两个复数相等的充要条件是“实部相等且虚部相等”.
三、例题讲析 例4 求下列等式中的实数a,b的值: (1) ; ; (2) ; ; (3)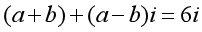
四、合作交流 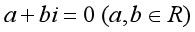 的充要条件是什么? 的充要条件是什么?
在复数的研究和应用中,常常用到共轭复数的概念. 五、抽象概括(二) 一般地,如果两个复数实部相等,而虚部互为相反数,则称这两个复数互为共轭复数. 复数 的共轭复数记作 的共轭复数记作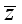 ,即:若 ,即:若 ,则 ,则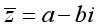 . . 例如:复数 的共轭复数是 的共轭复数是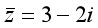 . .
|
学生活动
讨论 思考复数相等的条件
理解复数相等的条件
通过例题进一步加强对复数相等条件的认识
思考,讨论
掌握共轭复数的概念 |
教 学 过 程 |
教学内容 |
教 师 活 动 |
学生活动 |
六、例题讲析
|
六、例题讲析 例5写出下列复数的共轭复数: (1) ; ; (2)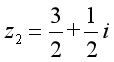 ; ; (3)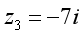 ; ; (4) 由例5的第(4)小题可看出,实数的共轭复数就是它本身.
复数是研究电学中交流电等理论的重要数学工具.用复数表示电压、电流、磁通等可使电学中各量的分析与研究变得简便. 如图9-1,是一个简单的电路图,E表示电源,R表示电阻,L表示感抗,C表示容抗,则线路的电流总阻抗Z可以用复数表示为  , ,
其中,j表示虚数单位i(注:在电学中i表示电流,为了与之相区分,电学中常用j表示虚数单位),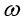 为角速度,且有 为角速度,且有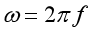 (f表示频率) (f表示频率)
 图9-1 图9-1
例6 在如图9-1所示电路中,求电压共振时,频率f与感抗L、容抗C之间的关系.
|
理解概念
了解复数在电工学上的应用
|
教 学 过 程 |
教学内容 |
教 师 活 动 |
学生活动 |
七、课内练习 八、课堂小结 |
七、课内练习 1.求下列等式中的实数a,b的值: (1)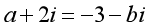 ; ; (2) ; ; (3)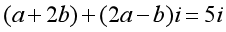 2.写出下列复数的共轭复数: (1) ; ; (2) ; ; (3) ; ; (4) . . 八、课堂小结 1. 复数相等的充要条件

2.共轭复数
若 ,则 ,则 . .
|
练习 进一步巩固知识点
讨论、交流、记忆
|
课后作业 |
对应的练习册上的习题 |
教后记 |
成功之处:本节课,由生活中数集的扩充引入课题,给出复数的概念,了解复数的实部、虚部、纯虚数等概念,会利用概念解决问题.在教学过程中,坚持面向全体学生,努力创设适合学生发展的数学教育. 与关注学习结果相比,更关注学生的学习过程.在教学过程中,由于学生已具备一定知识上的积累,采取自主与探究学习相结合的模式,借助多媒体使教师设计的问题与活动的引导密切结合,力图让学生亲历、感受并理解知识本身.强调学生“活动”的内化,通过学生的自主思考、表述及动手操作,调动了主动学习的积极性,学生在探究的学习过程中得以积极思考,掌握知识,以此达到使学生有效地对当前所学知识的意义建构的目的. 不足之处与改进措施:习题量与时间分配不足,导致学生课上练习不够充分,学生解答中存在各种问题强调不足.探究过程中环节紧扣,学生若课堂上不够积极主动,影响教学效果的达成.今后需要还需要将数学与专业课相结合,提高学生的学习兴趣. |
